也谈 "Knight Rush"
原问题来自Lox的文章http://cnlox.is-programmer.com/posts/34337.html。感谢之前Lox和我的交流,下面说说我的看法。
原题:
在一个国际象棋棋盘上(N*N),有一个棋子"马(Knight)",处在任意位置(x, y);马的走法是日字型,即其可以在一个方向上前进或后退两格,在另一方向上前进或后退一格。请编程找出马如何从位置(x, y)走到棋盘右下角(N, N)的位置的步骤。例如:假设棋盘大小为3*3,马处在(1,2)位置,马只需要走一步,即 (1,2)->(3,3)即可到达目的地。编程语言推荐的是Python,程序能输出一种可行的方法即可(无需找出所有方式),还有一些软件工程的要求诸如文档、注释、代码风格这些“无关痛痒”的东西。
下面我仅讨论算法相关的部分。
首先做一个假设:马知道自己在棋盘中的位置,也知道(N,N)的相对位置,棋盘格是连续的,没有障碍。后面都将基于该假设。
这可以归结为一个图搜索问题,用朴素的深度/广度优先搜索都能完成,但如果进行合理的剪枝,可以大大减少搜索的数量。就给出“一种可行的方法”而言,如果“可行”并不是指最短路径,是非常容易实现的。采用“贪心”的策略可以找到一个并不是太坏的解(不保证最优,即不保证最短路径,但已经足够快了)。方法是:
(1). 对于以(N,N)-(N-5, N-5)为对角线的正方形区域S内的所有点,找到从它到(N,N)的最短路径,并记录在一个表T中;
(2). 对于当前点P,若P在区域S中,则根据表T中的方法走到(N,N),算法结束,否则执行(3);
(3). 从P点出发的可以选方向中挑选一个,使得在该方向迈进一步后距离(N,N)最近,重复(2).
该算法的时间复杂度是O(N),对于大规模的N,这可以作为一个“可行”的算法,是否路径最短我并没有证明,但从直觉上说该算法所给出的路径与最短路径数相差不超过1-2. 即使该算法不保证给出最短路径,但在此基础上稍加改进(只是改进马走的最后几步)应该可以保证找到最短路径,这个任务就交给读者了,哈哈。
这显然不是最好的,无论从出题者还是解答者的角度来说,都希望得到最优算法,即在找出一条最短路径的前提下时间复杂度最小。O(N)似乎已经足够快了,是否还可以更快?
下面要说的算法并不基于图搜索,因为该问题太特殊——路径太规整,马也知道得太多,以至于是通过计算而不是搜索来得到答案.
首先,以(N,N)为原点重新建立坐标系,过原点水平向左为x轴,竖直向上为y轴。如下图所示。
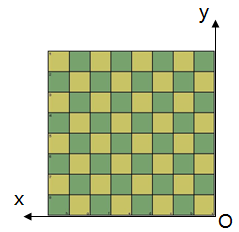
可以用下列方式重新描述原问题:
这是一个整数规划问题,其中x0,y0为起始点坐标,i1-i8为马从起始点跳回原点的过程中在8个方向上分别所需要跳的次数。8个方向如下图所示。
| 5 | 4 | ||
| 6 | 3 | ||
| 7 | 2 | ||
| 8 | 1 |
不妨再做两个假设:
ass1: x0≤y0,即起始点总在对角线y=x的上方,或在对角线上,对于起始点在对角线下方的情况实质是一样的,做一个对称变换即可;
ass2: 起始点足够远,x0>6, y0>6,对于较近的点可以事先建立最短路径表。
整数规划是NP问题,但其时间复杂度与变量个数(该问题为i1-i8共8个)紧密相关,而该问题的变量个数是固定的,只是x0,y0发生变化,对时间复杂度的影响不大。
直接套用整数规划的方法来解或许不好,因为变量数目仍然太多。事实上,可以进一步简化(i),因为i1-i8中两个相反的方向是没有必要同时存在的,那只会使路径更长,即ij与ij+4二者中至少有一个为0. 为简单起见,我们先讨论一种更特殊的情况,它对应起始点的一个子集,从该子集的每个点出发,只需i1和i2对应的两个方向的走动就可回到原点。下面将找出该子集,对(i)做简化,只保留i1,i2,则:
i1+2i2=x0,
该方程组完全确定i1和i2:i1=y0-(x0+y0)/3,i2=x0-(x0+y0)/3. 要使得i1,i2有意义,即
1. i1,i2非负,则y0≤2x0,由ass1知,x0≤y0≤2x0 (iii),
2. i1,i2为整数,则x0+y0能被3整除,即x0+y0≡0 (mod 3) (iv).
因此对于起始点的子集S={(x,y) | x0≤y0≤2x0, 且x0+y0≡0 (mod 3)},从该子集的每个出发,只需要在方向1上走i1次,再在方向2上走i2次便能回到原点。该走法是路径最短的,见(v).
举例:
对于起点(6,6), i1=i2=2,则最短路径可以是(6,6) → (4,2) → (0,0),或(6,6) → (2,4) → (0,0),其中每一直线都连续在一个方向上走了两步,当然还有别的走法,路径长度=(6+6)/3=4;
对于起点(5,7), i1=3, i2=1,则最短路径可以是(5,7) → (2,1) → (0,0),路径长度=(5+7)/3=4;
对于起点(9999998,10000000), i1=3333334, i2=3333332, 则最短路径可以是(9999998,10000000) → (6666664, 3333336) → (0,0),路径长度=(9999998+10000000)/3=6666666;
cond1: 一般的,对于起点(x0,y0)满足(iii)和(iv),一条可选的最短路径是(x0,y0) → (x0-i1,y0-2i1) →(0,0). 其路径的长度为i1+i2=(x0+y0)/3. 下图红线上的点满足该条件,由对应的i1+i2的值可知其最短路径长度.
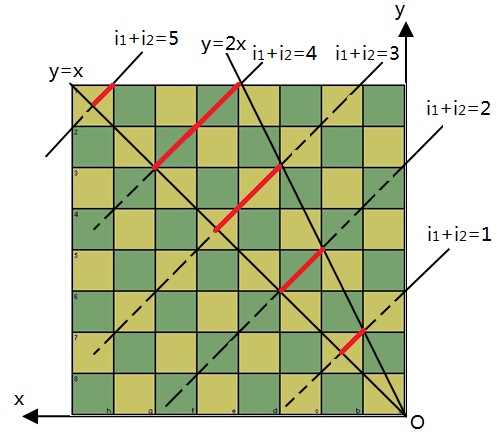
下面讨论其它情况,对大多数点而言,是不满足条件(iii)或(iv)的,但可以肯定的是,对于任意(x0,y0),以它作为起始点的路径长度的下界是:
证明:由(i)得:x0+y0=3i1+3i2+i3-i4-3i5-3i6-i7+i8 ≤ 3i1+3i2+3i3+3i4+3i5+3i6+3i7+3i8 =3z, => (x0+y0)/3 ≤ z, => (v) ≤ min(z),证毕.
因此,当不满足(iv)时,最短路径长度至少是[ (x0+y0)/3 ] + 1,其中[ ]表示向下取整.
对于不满足(iii)或(iv)的点,是不能只通过方向1和方向2的走动回到原点的,因此再增加两个方向7和8. 之所以不考虑方向3-6是因为除个别距离原点很近的点外,方向1,2,7,8完全能达到要求,而方向3-6只会使路径变得更长,由ass2,距离原点较近的点不在考虑范围内。在(ii)的基础上增加i7与i8, 得:
min z=i1+i2+i7+i8,
s.t.
i1+2i2-2i7-i8=x0,
2i1+i2+i7+2i8=y0.
i1,i2,i7,i8≥0. (vi)
由(vi)得:
z=i1+i2+i7+i8=(x0+y0)/3 + (4i7+2i8)/3, (viii)
3i1=(2y0-x0) - (4i7+5i8), (ix)
1. cond2: 若满足(iii)但不满足(iv)时,由(ix)和(x)知,可保证i1和i2非负. 此时i1+i2≡1 (mod 3), 或i1+i2≡2 (mod 3), 由(vii)知,
1). 若i1+i2≡1 (mod 3), 则只需再向方向8走一步,就能满足(iv),只要此时仍满足(iii) ,或(iii)的对称形式y0≤x0≤2y0,便可按cond1解答;
2). 若i1+i2≡2 (mod 3), 则只需再向方向7走一步,就能满足(iv),只要此时仍满足(iii) ,或(iii)的对称形式y0≤x0≤2y0,便可按cond1解答.
注:可以证明以上方法是最优的,因为沿7,或8走一步是必须的,否则无论如何不能回到原点;另外7或8也只能走一次,否则与cond1的结论相悖.
举例:
起点(8,9), 8+9=17≡2 (mod 3),应先沿7走一步,然后按cond1处理:(8,9) → (10,8) → (8,4) → (0,0),路径长度=1+(10+8)/3=7;
起点(50,50), 50+50=100≡1 (mod 3),应先沿8走一步,然后按cond1处理:(50,50) → (51,48) → (15,30) → (0,0),路径长度=1+(51+48)/3=34.
2. 若不满足(iii),即起始点在y=2x外,则可先通过方向7或方向8若干次,使得满足条件(iii). 至于若干次是多少次,可以由(x)确定,5i7+4i8≥y0-2x0, 但还是不能确定i7和i8的具体值,再考查(viii),要使得z最小,则4i7+2i8最小,可得:
min z'=4i7+2i8,
s.t.
5i7+4i8≥y0-2x0,
i7,i8≥0.
这是一个更小的规划问题,通过分析可得(可以通过平面坐标系分析,过程略),i7应尽量小,为0或1(若满足ass2,可以让i7=0),i8应尽可能大,也就是说尽可能沿方向8到达y=2x内,然后按cond1或cond2处理。
cond3: 对任意(x0,y0),满足y0>2x0,计算n=round_up((y0-2x0)/4),其中round_up是向上取整,沿方向8走n步. 计算d=x0+y0-n,若d≡0 (mod 3),则按cond1处理;若d≡1 (mod 3),则按cond2的1)处理;若d≡2 (mod 3),则按cond2的2)处理.
举例:
起点(0,7), n=2, d=5≡2 (mod 3),可选的最短路径为(0,7) → (2,3) → (4,2) → (0,0),路径长度=2+1+(4+2)/3=5;
起点(15,80), n=13, d=82≡1 (mod 3),可选的最短路径为(15,80) → (28,54) → (29,52) → (4,2) → (0,0),路径长度=13+1+(29+52)/3=41;
起点(0,8000000), n=2000000, d=6000000≡0 (mod 3),可选的最短路径为(0,8000000) → (2000000,4000000) → (0,0),路径长度为2000000+(2000000+4000000)/3=4000000.
结论:
算法描述如下:
1. 预计算以(0,0)-(6,6)为对角线的正方形内所有点的最短路径,并保存在表中;
2. 进行坐标变换,以右下角为原点;
3. 在新坐标系中,若对于起始点(x0,y0)满足y0<x0,则令x0'=y0,y0'=x0,将(x0',y0')作为新的起始点(最后输出路径时再变换回来);
4. 在新坐标系中,对于任意起点(始x0,y0),若同时满足(iii)和(iv),则按cond1处理,否则若在预计算的区域内,则查表找出最短路径,算法结束,否则执行5;
算法计算过程的时间复杂度是O(1),若要将最短路径输出,时间复杂度就根据输出数据的多少而定了.
代码我就不写了~~~
本人水平有限,难免有错漏和表述不清,欢迎讨论、质疑和改进,谢谢!
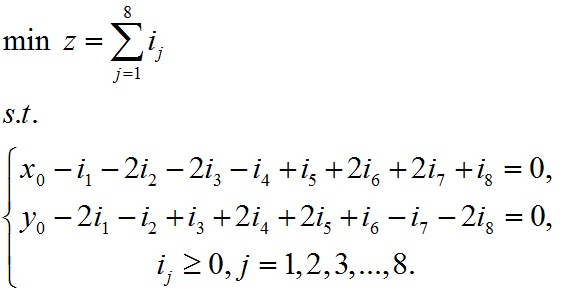
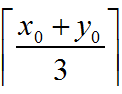
2013年3月10日 04:33
怎么变得那么窄,有空研究一下怎么调整,先这样吧。
2019年3月26日 08:07
Positive site. where did u come up with the information on this posting? I have read a few of the articles on your website now and I really like your style. Thanks a million and please keep up the effective work.